技术领域
本发明涉及一种双永磁同步电机混沌系统的滑模同步控制方法,特别是两个 初始条件不同且带有不确定参数的永磁同步电机混沌系统的同步控制方法。
背景技术
永磁同步电机(permanent magnet synchronous motor,PMSM)是一种典型的多 变量、强耦合非线性系统,在诸如机器人、航空飞行器以及伺服转台控制等高性 能系统中得到了广泛的应用。然而,近年来的研究表明,永磁同步电机在一定条 件下会呈现出混沌特性,混沌行为的存在将会产生不规则的电流噪声,严重影响 了系统的稳定运行,对PMSM的应用造成不便。然而,永磁同步电机中的混沌 运动并不总是有害的,在工业搅拌等一些应用场合,电机的混沌运动相反还被认 为是有益的并加以利用。永磁同步电机混沌同步是将两个永磁同步电机混沌系 统,即主系统和从系统的状态实现完全重构。由于混沌运动本身的特点,两个永 磁同步驱动电机的混沌同步有利于实现良好搅拌混合的延伸折叠,从而提高工业 搅拌的效率并减小搅拌过程中消耗的能量。
为了达到双永磁同步电机混沌系统的快速同步,许多有效的先进控制方法已 被引入。其中,滑模控制(sliding mode control,SMC)方法由于对系统数学模型要 求不高,且对系统参数摄动、外部扰动具有较强的鲁棒性,被广泛应用于混沌同 步控制研究中。但传统的滑模控制方法中由于控制增益的过高以及符号函数的存 在,导致其存在一定的抖振问题,影响了实际应用。为降低滑模控制中的抖振现 象,很多改进的滑模控制方法被提出,例如:高阶滑模、终端滑模、模糊滑模、 神经网络滑模等。
滑模控制作为一种重要的鲁棒控制策略,得到广泛的应用,运用滑模控制还可 实现多个具有相互关联的混沌系统的同步。滑模控制理论是一种算法简单、容易 实现且鲁棒性很强的方法,它可以在电机参数变化和出现外部扰动时仍能保持满 意的性能。本发明中应用主动滑模控制方法设计的控制器,可以实现永磁同步电 机从系统的状态快速跟踪永磁同步电机主系统的状态轨迹,最终实现双永磁同步 电机系统混沌状态的快速同步。
发明内容
本发明要克服双永磁同步电机在不同初始条件下呈现混沌特性且系统不确 定参数导致混沌状态不易快速精确同步的缺点,提供一种双永磁同步电机混沌系 统的滑模同步控制方法。采用主动滑模控制方法设计系统的同步控制器,改善系 统的跟踪性能,保证带有不确定参数的双永磁同步电机混沌系统可以实现状态同 步。
本发明的具体实现步骤如下
步骤1,建立如式(1)所示的永磁同步电机系统的混沌模型,初始化系统 状态以及相关控制参数;
其中,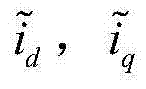 和
和 为状态变量,分别表示直轴和交轴定子电流以及转子角频率;
为状态变量,分别表示直轴和交轴定子电流以及转子角频率;
σ和γ为常值参数;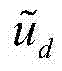 和
和 表示直轴和交轴的定子电压,
表示直轴和交轴的定子电压, 为外部扭矩,满足
为外部扭矩,满足
为使运算过程更简便,令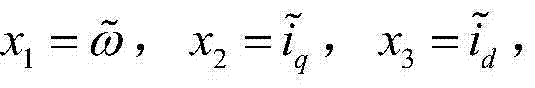 则永磁同步电机主混沌 系统如式(2)所示
则永磁同步电机主混沌 系统如式(2)所示
其中,x1,x2,x3是状态变量,σ和γ是系统参数。
永磁同步电机从混沌系统为被控系统,其表达式如下所示
其中,y1,y2,y3是状态变量,u1,u2和u3是控制信号。
步骤2,在每一采样时刻,计算式(2)和式(3)所示的永磁同步电机主从 混沌系统的同步误差、滑模面及其一阶导数;
2.1,定义同步误差为ei=yi-xi,i=1,2,3,则式(3)减去式(2)可以得到以下误 差系统
为便于计算,将式(4)可写成矩阵形式:
其中K为增益矩阵常数,
2.2,定义如下所示滑模面:
其中K为增益矩阵常数。
2.3,分别对式(5)等号两边进行求导,可得滑模面的一阶导数为
步骤3,根据同步误差e、滑模面s及其一阶导数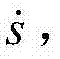 设计双永磁同步电 机混沌系统的同步控制器u(t);
设计双永磁同步电 机混沌系统的同步控制器u(t);
3.1,根据主动滑模控制策略,控制输入u(t)可用下面的表达式表示:
u(t)=H(t)-g(y)+g(x) (8)
其中H(t)是基于滑模控制规律设计的,虽然它有很多选择,但是为了不失一般 性,用下列公式表示:
H(t)=Kω(t) (9)
其中ω(t)为一个控制输入量,表达式为:
其中s=s(e)是一个产生期望动态的切换面。
3.2,把式(8)中的u(t)代入式(5),产生的动态误差为:
其中M(x,y)表示不确定参数,表示为:
M(x,y)=ΔAy+Δg(y)-ΔAx-Δg(x) (12)
设未知的非线性部分Δg(x),Δg(y)满足Lipchitz条件,即|M(x,y)|≤N|e|+B|x|, 其中N=(||ΔA||+L2),B=(L2+L1),L1,L2为大于0的正常数。为设计鲁棒控制器, 则Δg(x),Δg(y)必须满足Lipchitz的条件。这就需要使不确定项(B和N)是有 界的。即||B||≤βI,||N||≤ηI,其中β,η为正常数,I是单位对角矩阵,由于主系统 是有界的,因此M(x,y)是线性有界的。
3.3,计算式(6)和式(11)可得:
调整K使K+A所有特征根都有负实数部分,系统就会逐渐接近稳定状态。 可以使用常数加上比例的到达率,选择到达率为:
其中sgn(s)表示符号函数,并且常数r>0和常数q>0时,满足滑动条件,发生 滑模运动。
3.4,将式(13)和式(14)代入式(6)可得:
ω(t)=K-1(-q sgn(s)-rs+Ke-M(x,y)) (15)
因此,由式(8),式(9)和式(15),可得控制器u(t)的表达式为:
u(t)=-q sgn(s)-rs+Ke-M(x,y)-g(y)+g(x) (16)
3.5,设计李雅普诺夫函数 则可以证明
则可以证明 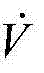 一定为负:
一定为负:
若满足条件式(17),则s是Lyapunov稳定的,这表明s有上界。根据式(17), 可知这个界限可通过增加r使之减少。即双永磁同步电机混沌系统的同步误差能 够收敛至滑模面s=0。
本发明的技术构思为:永磁同步电机在一定参数条件下呈现出混沌特性。针 对参数不确定的双永磁同步电机混沌系统,结合模控制理论,设计一种双永磁同 步电机混沌系统的滑模同步控制方法。采用主动滑模控制方法设计系统的同步控 制器,改善系统的跟踪性能,保证带有不确定参数的双永磁同步电机混沌系统可 以实现状态同步。本发明提供一种能够改善滑模控制抖振问题并提高系统控制精 度及鲁棒性的双永磁同步电机混沌状态同步控制方法,确保在系统参数不确定的 情况下,实现两个永磁同步电机混沌状态的快速同步控制。
本发明的优点为:算法效率高,能够在系统参数不确定的情况下提高控制精 度和鲁棒性。
附图说明
图1a为本发明的双永磁同步电机的主系统的混沌状态;
图1b为本发明的双永磁同步电机的从系统的混沌状态;
图2为本发明的同步控制算法的基本流程;
图3为本发明的双永磁同步电机混沌系统的同步响应曲线(t=10s控制器起 作用);
图4为本发明的双永磁同步电机混沌系统的同步误差曲线(t=10s控制器起 作用);
图5为本发明的控制器信号u1,u2和u3
具体实施方式
参照附图1-5,下面结合附图对本发明做进一步说明。
双永磁同步电机混沌系统滑模同步控制方法,包括以下步骤:
步骤1,建立如式(1)所示的永磁同步电机系统的混沌模型,初始化系统 状态以及相关控制参数;
其中,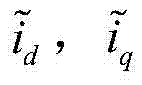 和
和 为状态变量,分别表示直轴和交轴定子电流以及转子角频率;
为状态变量,分别表示直轴和交轴定子电流以及转子角频率;
σ和γ为常值参数; 和
和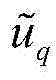 表示直轴和交轴的定子电压,
表示直轴和交轴的定子电压,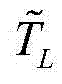 为外部扭矩,满足
为外部扭矩,满足
为使运算过程更简便,令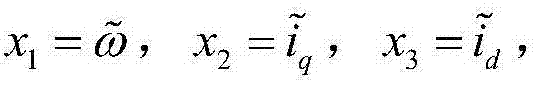 则永磁同步电机主混沌 系统如式(2)所示
则永磁同步电机主混沌 系统如式(2)所示
其中,x1,x2,x3是状态变量,σ和γ是系统参数。
永磁同步电机从混沌系统为被控系统,其表达式如下所示
其中,y1,y2,y3是状态变量,u1,u2和u3是控制信号。
步骤2,在每一采样时刻,计算式(2)和式(3)所示的永磁同步电机主从 混沌系统的同步误差、滑模面及其一阶导数;
2.1,定义同步误差为ei=yi-xi,i=1,2,3,则式(3)减去式(2)可以得到以下误 差系统
为便于计算,将式(4)可写成矩阵形式:
其中K为增益矩阵常数,
2.2,定义如下所示滑模面:
其中K为增益矩阵常数。
2.3,分别对式(5)等号两边进行求导,可得滑模面的一阶导数为
步骤3,根据同步误差e、滑模面s及其一阶导数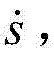 设计双永磁同步电 机混沌系统的同步控制器u(t);
设计双永磁同步电 机混沌系统的同步控制器u(t);
3.1,根据主动滑模控制策略,控制输入u(t)可用下面的表达式表示:
u(t)=H(t)-g(y)+g(x) (8)
其中H(t)是基于滑模控制规律设计的,虽然它有很多选择,但是为了不失一般 性,用下列公式表示:
H(t)=Kω(t) (9)
其中ω(t)为一个控制输入量,表达式为:
其中s=s(e)是一个产生期望动态的切换面。
3.2,把式(8)中的u(t)代入式(5),产生的动态误差为:
其中M(x,y)表示不确定参数,表示为:
M(x,y)=ΔAy+Δg(y)-ΔAx-Δg(x) (12)
设未知的非线性部分Δg(x),Δg(y)满足Lipchitz条件,即|M(x,y)|≤N|e|+B|x|, 其中N=(||ΔA||+L2),B=(L2+L1),L1,L2为大于0的正常数。为设计鲁棒控制器, 则Δg(x),Δg(y)必须满足Lipchitz的条件。这就需要使不确定项(B和N)是有 界的。即||B||≤βI,||N||≤ηI,其中β,η为正常数,I是单位对角矩阵,由于主系统 是有界的,因此M(x,y)是线性有界的。
3.3,计算式(6)和式(11)可得:
调整K使K+A所有特征根都有负实数部分,系统就会逐渐接近稳定状态。 可以使用常数加上比例的到达率,选择到达率为:
其中sgn(s)表示符号函数,并且常数r>0和常数q>0时,满足滑动条件,发生 滑模运动。
3.4,将式(13)和式(14)代入式(6)可得:
ω(t)=K-1(-q sgn(s)-rs+Ke-M(x,y)) (15)
因此,由式(8),式(9)和式(15),可得控制器u(t)的表达式为:
u(t)=-q sgn(s)-rs+Ke-M(x,y)-g(y)+g(x) (16)
3.5,设计李雅普诺夫函数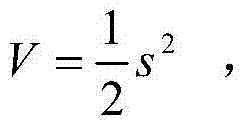 则可以证明
则可以证明 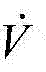 一定为负:
一定为负:
若满足条件式(17),则s是Lyapunov稳定的,这表明s有上界。根据式(17), 可知这个界限可通过增加r使之减少。即双永磁同步电机混沌系统的同步误差能 够收敛至滑模面s=0。
为验证所提方法的有效性,本发明对由式(2)表示的永磁同步电机主混沌系 统以及由式(3)表示的永磁同步电机从混沌系统的同步控制效果进行实验验证, 实验中控制器信号被设定为t=10s之后开始起作用。主从系统的初始状态设为 x1(0),x2(0),x3(0),=(20,0.01,-5)和y1(0),y2(0),y3(0),=(5,1,0.1);部分参数设置相同, 即:σ=5.46,γ=20;参数不确定项为ΔA=diag(0.1sin(t),0.1sin(t),0.1sin(t)), 控制器的参数设置为r=35,q=0.35,K=diag(-20,-10,-2)。
本发明提出的同步控制方法优越性体现在:从图3和图4的实验结果可以看 出,在主动滑模控制器的作用下,具有不确定参数的并且初始条件不同的双永磁 同步电机的混沌系统,各个状态在系统运行0.1秒钟左右便快速趋于同步,即两 个系统的同步误差趋于0。另外,从图5可以看出,控制信号基本没有抖振现象 发生。因此,本发明设计的控制方法不仅能够实现双永磁同步电机混沌系统同步 误差的快速收敛,并且能够有效抑制滑模控制信号的抖振问题。
以上阐述的是本发明给出的一个实施例表现出的优良优化效果,显然本发明 不只是限于上述实施例,在不偏离本发明基本精神及不超出本发明实质内容所涉 及范围的前提下对其可作种种变形加以实施。




 手机二维码
手机二维码 京公网安备11011302007134
京公网安备11011302007134