技术领域

本发明涉及运行模态分析技术领域，尤其是一种主轴系统运行模 态分析方法。

背景技术

主轴系统的动态特性对机床的加工精度和切削效率有直接影响， 准确掌握包含刀具-刀柄-主轴的主轴系统的模态参数是稳定性预测、 加工参数优化等的重要依据。通常在刀尖点施加激励并拾取响应，获 得刀尖点频响函数，再由试验模态分析获得系统模态参数。

然而由于刀具需不断更换，当主轴系统结构变化时，需要重新进 行试验，增加了测试时间。从在役结构的响应信号中获取模态参数的 运行模态分析方法，只需要利用响应数据便可进行参数辨识，其测试 结果比实验模态分析方法更接近结构的真实动力学行为。

从结构在役状态的振动响应信号中提取模态参数的工作模态分析 (Operational Modal Analysis，简称OMA)方法，识别的结构动态特性比 试验模态分析(Experimental Modal Analysis，简称EMA)更接近实际运 行条件下结构的真实动力学行为，成为近年来模态分析领域发展活跃 一个研究方向^[1]。但现有研究多基于激励信号为白噪声的假设，而切 削过程中存在由于主轴周期性旋转产生的谐波激励，给切削系统的 OMA分析造成困难，为此研究学者们发展了从切削过程响应数据中滤 除谐波成分的方法，如张义民等提出在工作模态分析时，利用概率密 度函数识别响应信号中周期强迫响应的方法，实现谐波模态与固有模 态的区分^[2]等。

目前基于环境激励的运行模态分析方法通常假设激励信号为零均 值白噪声信号。但是对于用于切削加工的主轴系统而言，切削振动信 号中存在由于主轴周期性旋转产生的刀齿通过频率、切削力周期频率 等复杂谐波，往往淹没包含动态特性信息的自由振动响应信号。虽然 可以通过从切削响应数据中滤除谐波成分的方法，获得结构的自由振 动响应来识别模态参数，但是由于谐波成分复杂，难以确定需要滤除 的频率成分，并且滤波和重构过程易破坏信号结构，易造成识别误差， 给主轴系统运行模态分析造成困难。为了在进行机床结构运行模态分 析时，能获得较强的宽频带随机激励，准确识别切削系统模态参数， 国内外学者提出通过切削特别设计的具有伪随机分布的突起或沟槽的 工件表面，以获得较强的宽频带随机激励的方法；使用单齿刀具断续 铣削狭窄工件以获得脉冲状切削力激励的方法；通过数控系统使主轴 以随机转速旋转，用单刃面铣刀切削单齿工件，以模拟随机激励等。 但是这些方法根据不同的机床以及感兴趣的频率范围，需要精心设计 被切削工件，试验成本较高且费时费力。因此，面向数控装备主轴系 统动态特性辨识的合理激励方式以及运行模态分析方法亟待研究。

发明内容

为了克服已有主轴系统模态分析方法的计算速度较慢、精确度较 低、误差控制较差、试验效率较低的不足，本发明提供一种能够实现 快速计算、精确度高、具有较好的误差控制、能够减少试验强度和时 间、大幅提高试验效率的基于脉冲激励响应信号互功率谱函数的主轴 系统运行模态分析方法。

本发明解决其技术问题所采用的技术方案是：

一种基于脉冲激励响应信号互功率谱函数的主轴系统运行模态分 析方法，包括以下步骤：

1)在主轴系统的刀柄上分别选取激励点，利用钢锤在选取的激励 点对主轴系统实施脉冲激励；

选取距离激励点较近且响应信号幅值较大的响应点作为参考点；

在所述参考点及反映主轴振型的各关键几何模型节点布置响应测 点；

2)采集所述参考点和响应点在脉冲激励后产生的响应信号；

3)对采集信号进行带通滤波，其通频带为感兴趣的结构模态频率 范围，对所有响应通道加汉宁窗；

4)求取参考点与响应点之间的互功率谱函数，并构建互功率谱函 数不同采样时刻数据构成的矩阵方程；

5)利用所述矩阵方程求解系数矩阵，得到系统极点；

6)识别模态振型及模态参与因子矩阵；

7)进行模态置信判据矩阵值计算，如果模态置信判据值不佳，则 选取不同采样时刻值，返回到步骤4)重新构建矩阵方程组，直至模 态置信判据值在预设合理区间以内，获得主轴系统模态参数。

进一步，所述方法还包括以下步骤：8)模态动画绘制：得出各点 每个方向的模态振型矢量，与测点布置几何模型对应，就得到描述各 测点x、y、z方向上的相对振幅的模态振型动画。

本发明的有益效果主要表现在：1、能够实现快速计算、精确度高、 具有较好的误差控制、能够减少试验强度和时间，大幅提高试验效率； 2、突破了已有实验模态分析技术要求外加激励响应输入和对激励输入 各种强制假设的缺陷，可实现在工作现场方便快速地对数控加工设备 的主轴系统进行动态特性分析，而且可以得到有些在实验室激励条件 下不能得到的振型；3、不需要测量外部激励，只测量响应数据，减少 了设备需求，试验成本可以大大降低，为主轴系统运行模态分析理论 和技术增添了一种新方法。

附图说明

图1为本发明流程示意图。

图2为主轴系统运行模态分析系统组成示意图。

图3为主轴系统测点及激励点布置示意图。

图4为模态参数识别稳态图。

图5为模态参数的MAC矩阵图。

图6为识别的主轴系统模态振型图，其中，(a)是一阶振型，(b) 是二阶振型，(c)为三阶振型，(d)为四阶振型。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图6，一种基于脉冲激励响应信号互功率谱函数的主轴 系统运行模态分析方法，包括以下步骤：

1)在主轴系统的刀柄上选取激励点，利用钢锤在选取的激励点对 主轴系统实施脉冲激励；

选取距离激励点较近且响应信号幅值较大的响应点作为参考点；

在所述参考点及反映主轴振型的各关键几何模型节点布置响应测 点；

2)采集所述参考点和响应点在脉冲激励后产生的响应信号；

3)对采集信号进行带通滤波，其通频带为感兴趣的结构模态频率 范围，对所有响应通道加汉宁窗；

4)求取参考点与响应点之间的互功率谱函数，并构建互功率谱函 数不同采样时刻数据构成的矩阵方程；

5)利用所述矩阵方程求解系数矩阵，得到系统极点；

6)识别模态振型及模态参与因子矩阵；

7)进行模态置信判据矩阵值计算，如果模态置信判据值不佳，则 选取不同采样时刻值，返回到步骤4)重新构建矩阵方程组，直至模 态置信判据值在预设合理区间以内，获得主轴系统模态参数。

进一步，所述方法还包括以下步骤：8)模态动画绘制：得出各点 每个方向的模态振型矢量，与测点布置几何模型对应，就得到描述各 测点x、y、z方向上的相对振幅的模态振型动画。

参见图2，本发明的主轴运行模态分析系统，包括主轴1、刀柄2、 加速度传感器3、刀具4、钢锤5、数据采集前端6、移动工作站7。 利用LMS SCADAIII系统，用加速度传感器3测试主轴系统各测点的 振动加速度-时间数据，各加速度传感器3分别与数据采集前端6电连 接，数据采集前端6与移动工作站7电连接，。加速度传感器3采集到 多点脉冲激励下的响应信号后，将其传入数据采集前端6，再传到移 动工作站7，所采集的振动响应信号数据通过数据采集前端导入运行 模态分析软件模块进行分析处理，(参见图2)，识别模态参数，具体 操作步骤如下：

1)选择激励点

为了识别主轴系统的模态参数，应尽可能对数控装备输入一个宽 频随机激励信号。脉冲激励的自功率谱与白噪声信号相近，即其谱密 度在较低频率段接近于平直，是较理想的激励信号。因此，可以利用 钢锤对主轴系统施加脉冲激励，以激发主轴系统的各阶模态。

在本发明所述的技术方案中，“脉冲激励”是指在主轴系统刀柄上 选取激励点，以保证激励能量均匀输入至主轴系统各部件，充分激励 结构的模态振型，提高采集信号的信噪比。参见图3，以刀具上下运 动方向为z轴，以加工进给运动方向作为x轴建立笛卡尔坐标系。在 主轴及球头铣刀上共布置19个测点，其中主轴和刀柄上各布置8个测 点，每90度布置一个测点，球头铣刀上布置3个测点。由于多点激励 时能量在系统中分布较均匀，既能充分激励结构的各阶模态，又可改 善单点激励时的非线性和信噪比低等现象，达到对主轴系统的有效激 励，且对于密集模态和重根情况有很强的识别能力，降低模态丢失的 可能性，因此选择刀柄上的8号点进行脉冲激励。

2)选择参考点和响应点，测取结构振动响应

在本实施例中，在待测主轴系统选取刀柄上8号点作为参考点和 18个响应点，同时在参考点和响应点上分别固定加速度传感器3。通 过加速度传感器3采集脉冲激励下参考点及各响应点的振动加速度。

3)求取互相关函数，并将其表示为复模态形式

互相关函数表示的是两个时间序列之间和同一个时间序列在任意 两个不同时刻的取值之间的相关程度，即互相关函数是描述随机信号 x(t),y(t)在任意两个不同时刻t₁，t₂的取值之间的相关程度。按照式(1) 计算结构响应点j和参考点i之间的互相关函数

$R_{\mathrm{ij}}\left(\mathrm{\τ}\right)={\∫}_o^T{x}_i\left(t\right)x_j(t+\mathrm{\τ})\mathrm{d\τ}---\left(1\right)$

式中，R_ij(τ)为响应点j和参考点i之间的互相关函数，T为测试 时间，x_i(t)为参考点的加速度响应信号，x_j(t)为响应点的加速度响应 信号，τ为时间间隔。

对结构响应点j和参考点i之间的互相关函数R_ij(τ)按照时间间隔Δt 采样，并将其表示为复模态形式

$R_{\mathrm{ij}}\left(\mathrm{k\Δt}\right)=\underset{r=1}{\overset{N}{\mathrm{\Σ}}}{C}_{\mathrm{rij}}{e}^{{\mathrm{\λ}}_r\mathrm{k\Δt}}---\left(2\right)$

式中C_rij为与第r阶模态相关的常系数；N为待识别模态阶数；Δt为采 样时间间隔；λ_r为系统极点。

将系统极点λ_r表达为${\mathrm{\λ}}_r=-{\mathrm{\ξ}}_r{\mathrm{\ω}}_r\±{\mathrm{j\ω}}_r\sqrt{1-{\mathrm{\ξ}}_r^2}---\left(3\right),$式中ξ_r为第r阶模 态阻尼比；ω_r为第r阶模态无阻尼固有频率。

4)求取响应信号互功率谱函数，构建由不同采样时刻的互功率谱 函数值构成的矩阵方程。

将R_ij(kΔt)作周期延拓，并进行离散傅里叶变换(DFT)，得到响应 点j和参考点i之间单边互功率谱密度函数：

$S_{\mathrm{ij}}^{+}\left(\mathrm{k\Δt}\right)=\frac{1}{N}{\mathrm{\Σ}}_{k=1}^{2N}{\mathrm{\Σ}}_{r=1}^N{R}_{\mathrm{ij}}\left(\mathrm{k\Δt}\right)e^{(-\mathrm{j\πkr}/N)}---\left(4\right)$

取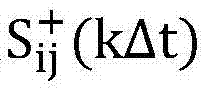在不同采样起始时刻的值建立互功率谱函数矩阵方程：

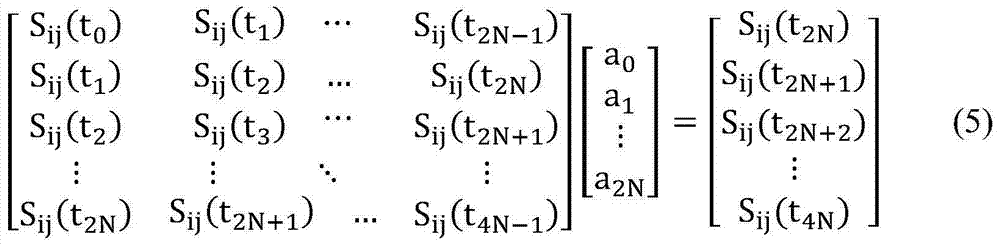
式中a₀，a₁，…a_2N为系数；S_ij(t₀)，S_ij(t₁)…S_ij(t_4N)为响应点j 和参考点i之间互功率谱函数在t₀，t₁,…t_4N时刻的取值。利用该方程 组的协方差矩阵构成压缩方程，得到该超定方程的最小二乘解，得到 系数a₀，a₁，…a_2N的取值。

5)识别系统极点

为识别系统极点，令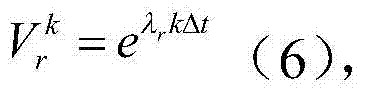构造下列方程：

${\mathrm{\Σ}}_{k=1}^{2N}{a}_k{S}_{\mathrm{ij}}^{+}\left(\mathrm{k\Δt}\right)={\mathrm{\Σ}}_{k=1}^{2N}\left(a_k{\mathrm{\Σ}}_{r=1}^N{C}_{\mathrm{rij}}{V}_r^k\right)={\mathrm{\Σ}}_{r=1}^N\left(C_{\mathrm{rij}}{\mathrm{\Σ}}_{k=1}^{2N}{a}_k{V}_r^k\right)=0---\left(7\right)$

式中a_k为系数，上式左边由2N项相加而成，因此方程组特征解 的个数至少应等于2N，因此k＝0,1,2…2N。上式如果成立，则系数 a₀,a₁,…a_2N满足下列有理分式正交多项式即Poroney多项式方程，且 该多项式以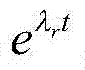为特征解。取a_2N＝1，得到：

$a_0+a_1{V}_r^1+...+a_{2N-1}{V}_r^{2N-1}+V_r^{2N}=0---\left(8\right)$

将估计出的系数矩阵a₀，a₁，…a_2N代入式(8)，求得系统的极点。

6)识别模态振型及模态参与因子矩阵

将互功率谱函数矩阵表示为系统各阶模态振型和模态参与因子矩阵的 部分分式之和，得到

$\left[S_{\mathrm{ij}}^{+}\left(\mathrm{k\Δt}\right)\right]=\underset{r=1}{\overset{N}{\mathrm{\Σ}}}[\left(V_r\right)e^{{\mathrm{\λ}}_r\mathrm{k\Δt}}\left(L_r\right)+\left(V_r^{*}\right)e^{{\mathrm{\λ}}_r^{*}\mathrm{k\Δt}}\left(L_r^{*}\right)]---\left(9\right)$

式中，V_r为模态振型矩阵，L_r为模态参与因子矩阵，表示在系统响应 中各阶模态的贡献量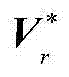，为模态振型矩阵的复共轭矩阵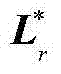，为模态参 预因子矩阵的复共轭矩阵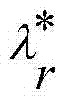，为系统极点的共轭复数；

将识别的系统极点代入式(9)，求得由各阶模态振型矢量Ψ_r构成的 模态振型矩阵V_r及其模态参与因子矩阵L_r，获得系统模态参数的全局 估计。

在本实施例中，采用最小二乘复频域法(LSFD方法)考察不同计算 阶次下各阶模态对应的固有频率、阻尼比及模态振型的计算误差。为 了实现当计算阶次增加时最小二乘误差能快速收敛，设定识别时的频 率误差为2％，阻尼比误差为5％，振型误差为2％。如果增加计算阶 次后，得到的极点和留数基本不变，则在该频率处标注符号“S”，如果 只有频率不变，则注上“f”，如果只有阻尼比不变，则标注“d”，只有 留数不变则注上“V”，得到如图4所示的最小二乘误差稳态图，选取 在所有计算阶次上标注“S”点最多的N列所对应的频率为系统模态频 率，并由此计算出系统阻尼比及模态振型。

7)模态验证和分析：主要完成运行模态分析结果的正确性检验。 利用模态置信判据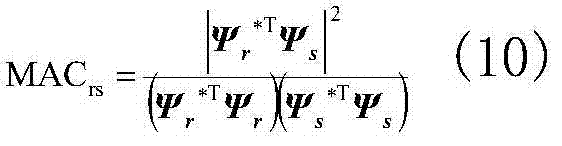判断模态估计的准确性。其 中Ψ_r为第r阶模态振型矢量；Ψ_s为第s阶模态振型矢量；Ψ_r^*T为第r 阶模态振型矢量的共轭转置；Ψ_s^*T为第s阶模态振型矢量的共轭转置。 通过模态置信判据MAC矩阵可判断模态参数拾取结果的正确性，从而 判断模态估计的准确性。如果两模态振型之间存在线性关系，其MAC 值接近于1，如果它们是彼此无关的，则MAC值接近于零。经过模态 置信判据矩阵判断识别结果的正确性，如果各阶模态间的MAC值均在 合理区间内，则识别的各阶模态为真实模态，识别结果准确，结束整 个运算过程，利用该方法识别的模态参数的MAC矩阵如图5所示。如 果存在某两阶模态间的MAC值不在合理区间内，则从步骤(4)开始， 选择不同采样时刻数据重新计算直至符合要求为止。这样确定了各阶 模态参数值，基于多点脉冲激励的运行模态分析核心计算过程结束。

8)模态动画绘制：得出各点每个方向的模态振型矢量，与测点布 置几何模型对应，就得到描述各测点x、y、z方向上的相对振幅的模 态振型动画，从而完成整个运行模态分析全过程。识别的主轴系统前 四阶模态振型图参见图6。

所述步骤2)中参考点和响应点的振动加速度由加速度传感器3 测量，由数据采集前端6完成振动加速度的记录。

所述步骤7)中，利用模态置信判据进行识别结果的正确性检验。

上所述仅是本发明的较佳实施方式，故凡依本发明专利申请范围 所述的构造、特征及原理所做的等效变化或修饰，均包括于本发明专 利申请范围内。

以上所述仅是本发明的优选实施方式，本发明的保护范围并不局 限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保 护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离 本发明原理前提下的若干改进和润饰，这些改进和润饰也应视为本发 明的保护范围。