技术领域

本发明涉及无线通信技术领域，具体涉及一种HARQ-IR在相关莱斯衰落场景下的吞吐量最大化设计方法。

背景技术

混合自动重发请求(HARQ)是一种非常有效保障可靠性的传输技术，在各种无线通信系统中被广泛采用。近年来，HARQ技术在莱斯衰落场景下的应用已经吸引了越来越多研究人员的关注，特别是在轻阴影衰落场景下(例如购物中心、卫星/飞机对地通信)存在很强的直视路径分量。值得一提的是，当直视分量消失时，莱斯衰落信道退化为瑞利衰落信道，在相关或独立的瑞利衰落信道上的HARQ方案已被广泛研究。忽略直视路径的影响会显著高估系统性能，因此会对系统的性能和优化设计产生错误指导。对此，研究HARQ系统在莱斯衰落信道上的性能是非常必要的，也是进行HARQ系统的优化设计所不可或缺的一部分。利用有限状态信道模型，Pimentel等人研究了在莱斯衰落信道下的I类型HARQ的错误检测概率，并在此基础上检测了各种系统参数对吞吐量性能的影响。根据信息论，由于I类型HARQ与分集合并中选择合并具有相同形式的信噪比(SNR)，因此它们的性能等价，而在莱斯信道条件下对于选择合并的研究，前期文献已经进行了广泛讨论，因此这些研究成果同样适用于I类型HARQ。

然而对于追加合并HARQ(HARQ-CC)和增量冗余HARQ(HARQ-IR)两种类型来说，分析这两种类型的HARQ在相关莱斯衰落信道下的系统性能时，分别会涉及到处理多个相关偏离随机变量的和以及乘积，目前来说处理这些数学问题还是有相当的难度和挑战。然而，HARQ-CC本质上是最大比合并(MRC)的应用，因此前期的研究成果也适用于HARQ-CC。但遗憾的是，已有研究领域中还没有现成的方法可用于分析一般莱斯衰落信道上的HARQ-IR的性能，唯一针对HARQ-IR的研究是基于准静态莱斯衰落信道，推导对应的中断概率和吞吐量，其中准静态衰落信道假设每次传输过程信道响应是恒定的。这种假设由于仅处理单个随机变量，显然过于简化了分析，而在广义莱斯衰落信道上对应的结论并不适用。因此有必要讨论在任意相关性莱斯衰落信道上的HARQ-IR的性能，它包含了直视分量和时间相关性的影响。根据相关莱斯信道状态信息的统计特征，本发明针对HARQ-IR设计一种吞吐量最大化的功率和速率优化选择方案。

发明内容

本发明的目的是为了解决现有技术中的上述缺陷，提供一种增量冗余混合自动重发请求(HARQ-IR)在相关莱斯衰落场景下的吞吐量最大化设计方法。

本发明的目的可以通过采取如下技术方案达到：

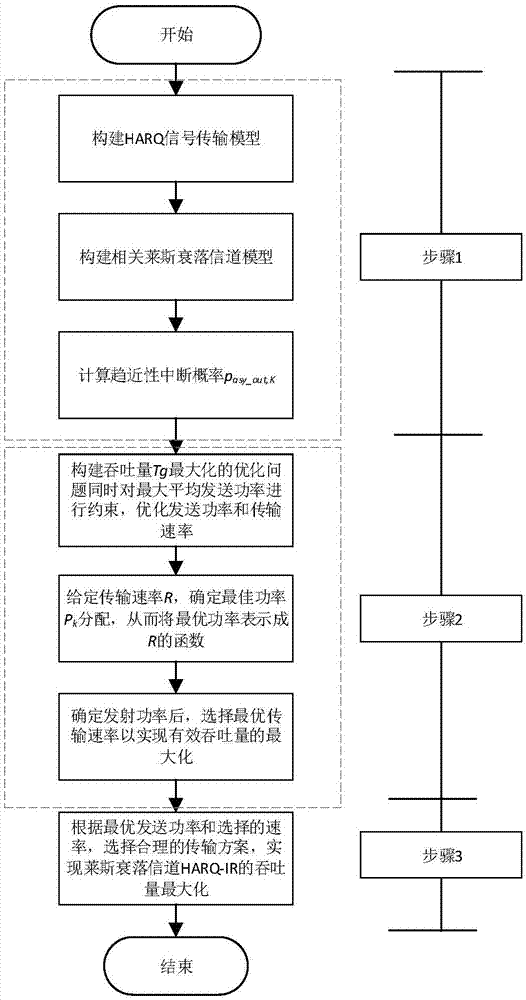
由于HARQ的性能取决于中断概率性能指标，因此首先计算HARQ-IR在相关莱斯衰落信道上的中断概率，这也是进行HARQ-IR系统优化设计必不可少的步骤。为了获得简单闭合形式的中断概率，可以渐进分析在高信噪比条件下中断概率的表达式，分析中须体现直视路径和时间相关性对中断概率的影响。基于构建的吞吐量最大化问题，结合得到的中断概率的简单闭合形式，进行最优发送功率和传输速率的求解，最后利用最佳发送功率和最优传输速率来合理选择实际中的调制和编码方案。吞吐量最大化的设计框图如图1所示，技术方案实施步骤如图2示，包括三个步骤，每个步骤具体描述如下：

步骤S1、根据信道状态信息的统计特征推导趋近性中断概率；

HARQ-IR在相关莱斯衰落场景下的吞吐量最大化的优化设计方案中，由于吞吐量表达式决定于中断概率，因此首先根据莱斯衰落信道状态信息的统计特征推导中断概率，可细分为以下三个步骤：

S101、构建HARQ信号传输模型。根据HARQ-IR机制，每个原始信息消息首先被编码为一个长码字，然后被均分割成K个子码字，其中K表示最大可允许传输次数。满足块衰落条件下，第k个子码字x_k的所有符号在传输中遭受相同衰落，第k轮所接收到的信号y_k为：

y_k＝h_kx_k+n_k，

其中，h_k表示信道响应，n_k表示复加性高斯白噪声，且具有零均值和协方差矩阵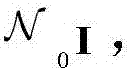即

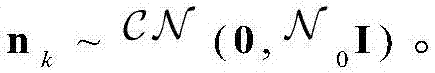
S102、构建相关莱斯衰落信道模型。h_K＝(h₁,...h_K)表示相关莱斯衰落信道响应向量，h_K服从期望向量和协方差矩阵为h_L,K＝(h_L,1,...,h_L,K)和

C_K＝E((h_K-h_L,K)(h_K-h_L,K)^H)＝E(h_Kh_K^H)的多变量圆对称正态分布，其中h_L,K表示直视路径分量。

S103、趋近性中断概率计算。当信噪比趋于无穷大时，即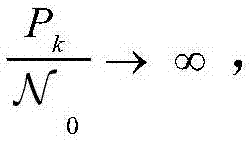经过K次传输后中断概率渐进表达式可以表示为

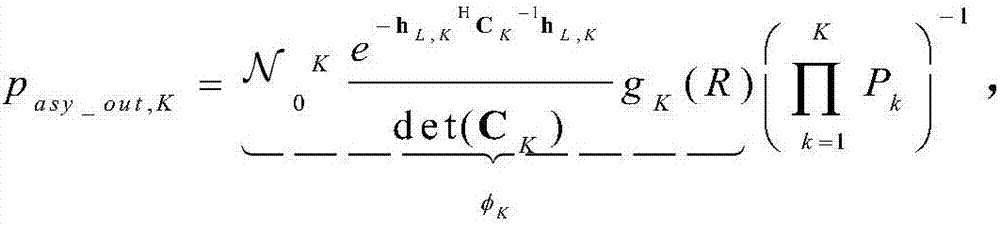
其中，P_k表示第k次传输的信号发送功率，R为预定的信号传输速率，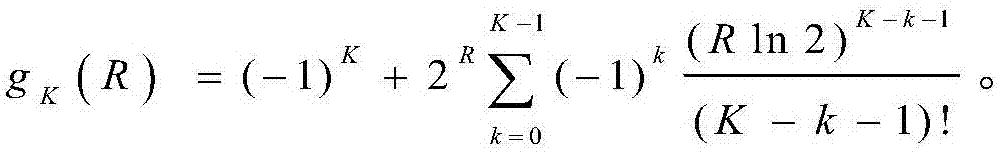

步骤S2、构建吞吐量最大化的优化问题并求解；

在相关莱斯衰落场景下最大化HARQ-IR的吞吐量方案中，衡量单次HARQ传输的吞吐量的性能指标是有效吞吐量T_g＝R(1-p_out,K)。此外，在最大化吞吐量的同时，需要对最大平均发送功率进行约束以保障能量效率。通过优化发送功率和传输速率来实现吞吐量最大化，优化问题可以构建成：

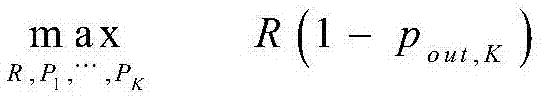
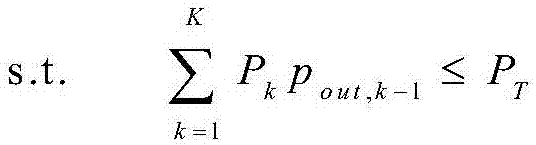
P₁,…,P_K≥0

R≥0

式中，p_out,k表示经过k次传输后的系统中断概率，P_T表示平均发送功率最大阈值，鉴于上述优化问题的特殊形式，可以将吞吐量最大化问题依次分解成最佳功率分配与最优速率选择，求解步骤如下：

S201、最佳功率分配。在给定固定传输速率R，发送功率P₁,…,P_K的优化可以重新表述为如下的最小化约束问题：

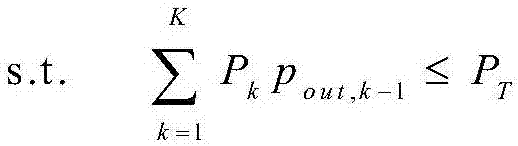
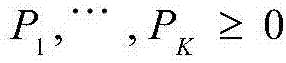
将步骤S1中获得的中断概率渐近表达式代入到上述优化问题中，最优发送功率可以表示成

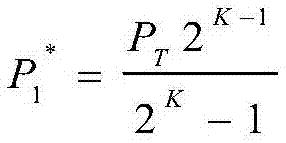
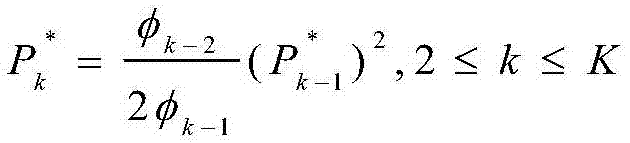
S202、最优速率选择。确定最佳发送功率之后，最佳发送功率均表示成传输速率函数，因此将最佳发送功率带入原始优化问题中，最后优化问题蜕变成最优速率选择，即：

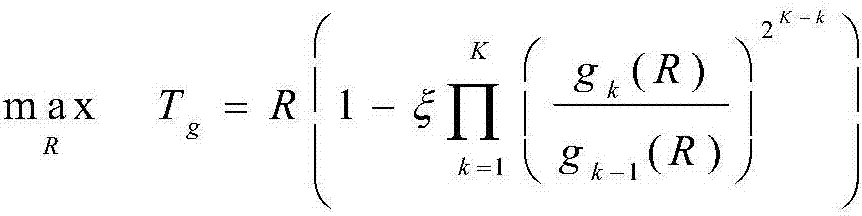
s.t.R≥0.

其中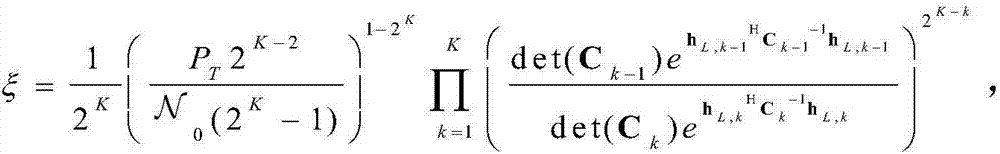，利用一维穷搜索可以求解最优传输速率。

S203、最优速率近似闭合求解。利用T_g的上下界来降低最优传输速率的计算复杂度，具体如下：

S2031、将吞吐量T_g替换为上/下界T_a(R)，当a＝L表示吞吐量下界，a＝R表示吞吐量上界。即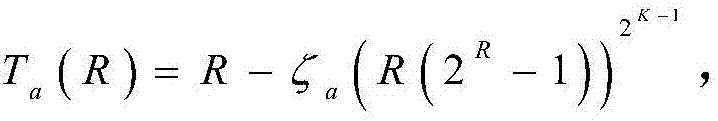

其中，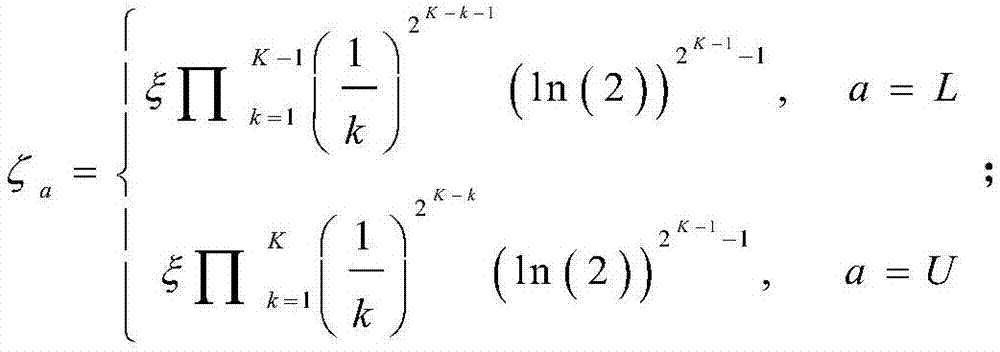

S2032、利用吞吐量上下界，可以将原始最优化问题缩放成：

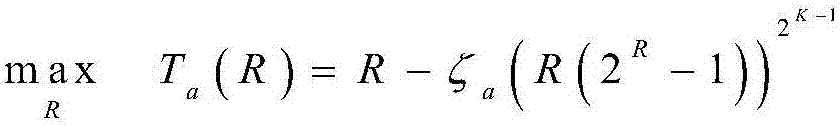
s.t.R≥0.

S2033、吞吐量上下界所对应的最优传输速率为ψ_a(R)的零点，即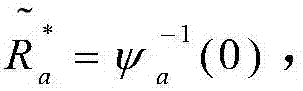其中，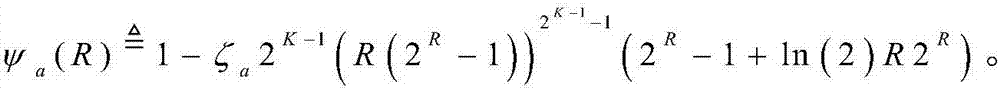

步骤S3、实际传输方案合理选择；

根据最佳发送功率和最优传输速率表达式，合理选择编解码方案和自适应选择调制技术。

进一步地，所述的步骤S203中所推导的有效吞吐量上下界是根据不等式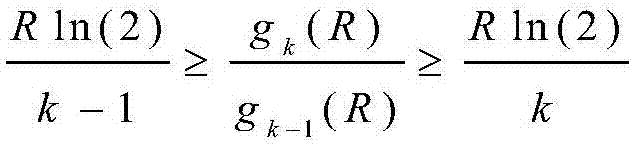所获得。

进一步地，所述的步骤S203中上下界所对应的最优吞吐量与真实最优吞吐量之间满足关系为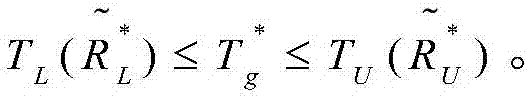

进一步地，所述的步骤S203中函数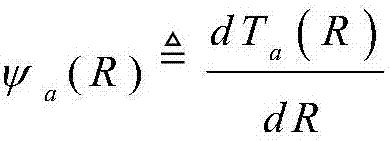是单调递减函数，其零点唯一存在且通过二分法进行快速数值计算。

进一步地，所述的步骤S2中所得到的最优吞吐量在高信噪比条件下，最优吞吐量遵循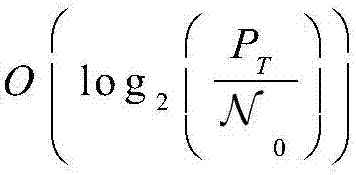的标度定律，斜率是2-2^1-K。

进一步地，所述的步骤S2中直视路径分量对所得到的最优吞吐量产生正面影响，而时间相关性对所得到的最优吞吐量会产生负面影响。

本发明相对于现有技术具有如下的优点及效果：

1、考虑到中断概率是最基本的性能指标，本发明试图对高信噪比下的中断概率进行渐近性分析。渐近中断概率的闭合形式不仅量化了直视路径和时间相关性的影响，而且其简单表达式可以分别系统的优化设计，将有助于本发明实现有效吞吐量最大化，其中有效吞吐量是衡量HARQ的平均吞吐量的重要指标。

2、通过约束最大平均发送功率，联合选择最佳发送功率和传输速率来最大化系统吞吐量。应用分解理论，将吞吐量最大化问题转化为单变量优化问题，大大降低了计算复杂度。

3、此外，从优化结果可以观察到一些非常有意义的结果，如最优吞吐量相对于信噪比(SNR)的标度定律、时间相关性对最优吞吐量的负面影响以及HARQ-IR的系统性能可以受益于直视路径。这些直接的结论将对HARQ-IR的系统设计有非常深远的指导意义。

附图说明

图1是本发明的系统框图；

图2是本发明吞吐量最大化算法流程图；

图3是本发明中渐进中断概率的验证图；

图4是本发明吞吐量最大化算法与均匀功率分配算法的性能比较图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例

本实施例考虑HARQ-IR在相关莱斯衰落信道下的应用。根据HARQ-IR机制，每个原始信息消息首先被编码为长码字，然后被均等分割成K个子码字，其中K表示传输的最大可允许数量。K个子码字每次传输将被依次传递，直到接收端成功解码该消息。值得一提的是，接收端应用码合并技术用于信号接收，具体来说就是将前面错误接收的子码字与当前接收的子码字合并用以联合解码。基于解码成功与否，接收端将反馈二进制肯定/否定确认信息(ACK或NACK)以通知发送端。将x_k定义为第k个子码字,同时假设信号传输遭受块衰落，这意味着x_k的所有符号在第k次传输中经历相同的信道实现。因此，在第k轮HARQ中接收到的信号可以表示成：

y_k＝h_kx_k+n_k(1)

其中n_k表示具有零均值和协方差矩阵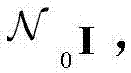即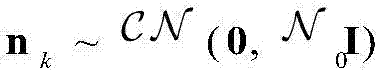的复加性高斯白噪声(AWGN)矢量，I代表一个单位矩阵；h_k表示第k次传输中的信道脉冲响应。在轻阴影衰落和中低速移动性环境下，与以往研究不同，这里考虑时间相关性和直视链路来准确分析HARQ-IR的性能，它们显然会影响HARQ-IR优化设计。为建立相关莱斯分布，这里定义信道响应向量h_K＝(h₁,...h_K)，其中h_K遵循期望向量和协方差矩阵为h_L,K＝(h_L,1,...,h_L,K)和C_K＝E((h_K-h_L,K)(h_K-h_L,K)^H)＝E(h_Kh_K^H)的多变量圆对称正态分布。其中h_L,K代表直视分量，h_K＝h_K-h_L,K代表散射分量，符号(·)^H和det(·)分别表示共轭转置和行列式的运算。为了反映直视分量相对于散射分量的强度，定义第k个信道系数的莱斯因子为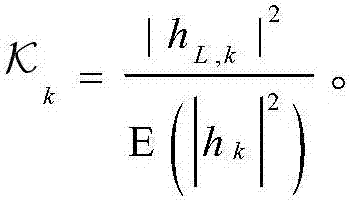h_K的联合概率密度函数(PDF)由下式给出：

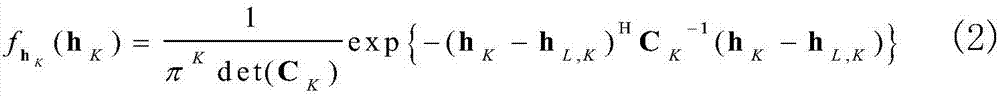
根据(1)，第k轮HARQ传输所接收到信号的SNR可以表示成:

其中，P_k表示用于第k次HARQ传输的发送功率。

1、渐近中断概率

中断概率是评估HARQ系统性能的最重要性能指标。通过将实现信道编码的信息理论容量应用于HARQ-IR，HARQ-IR通过采用能获得最大信息论容量的编码，中断事件发生在当信道累积互信息量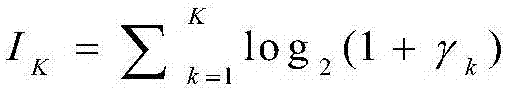低于传输速率R时。因此在经过K次HARQ传输之后，中断概率由下式给出：

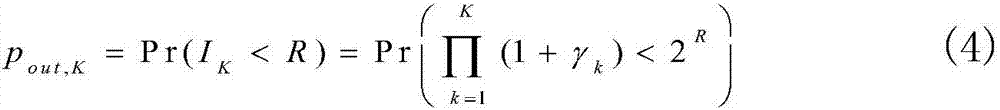
因此计算中断概率p_out,K最终转化成计算多个移位信噪比的乘积的分布。然而，衰落信道之间的时间相关性导致了信噪比相关，因此在推导p_out,K数学表达式时会涉及到多重积分，这显然会对分析和计算造成很大挑战。更具体地说，将(3)代入至(4)中可得出：

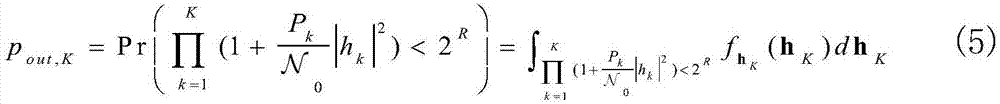
其中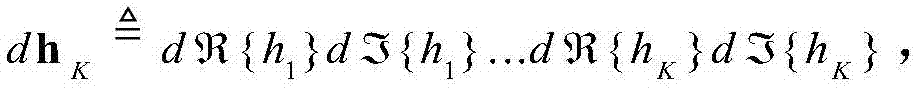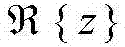，和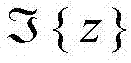分别表示复数z的实部和虚部。在之前大量文献讨论中均是分析时间相关瑞利或Nakagami-m衰落信道下的HARQ-IR的中断概率，而在本发明中的信道模型(2)不但考虑了信道之间的相关性，同时还考虑了直视链路的影响，这将极大地阻碍了p_out,K的数学推导。由于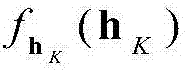的复杂形式，通过(5)中的积分来获得p_out,K的精确表达式几乎是不可能的。因此，本发明将在高信噪比条件下进行渐近中断概率分析，从而提供一个紧凑且有意义的中断概率表达式。

当SNR趋于无穷大，即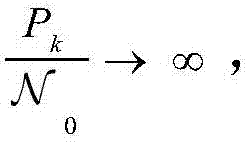在(5)中积分域

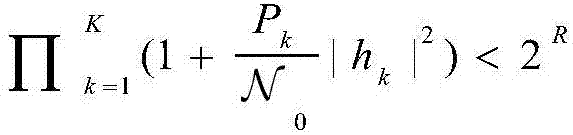表明|h_k|²→0。于是可以得到：

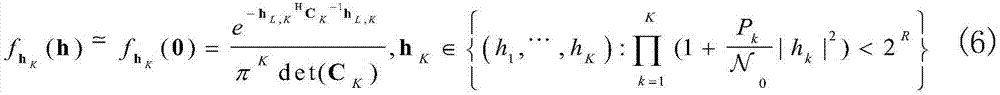
其中，符号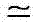表示“渐进式等于”。因此，(5)可以改写为:

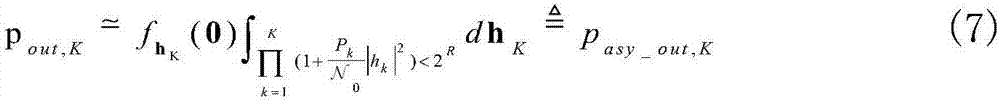
其中，p_{asy_out,K}是高信噪比下渐近中断概率。根据h_K和dh_K的定义，p_{asy_out,K}可以继续表示成

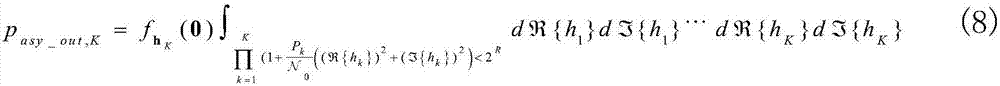
利用极坐标变换，即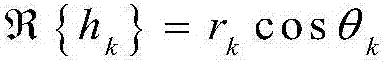和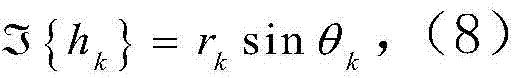式可进一步表示成：

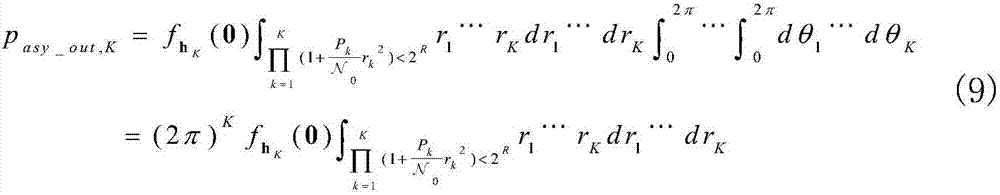
再进行变量代换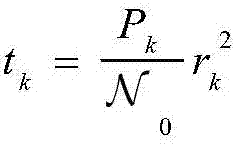和k∈[1,K]，(9)可以简化为：

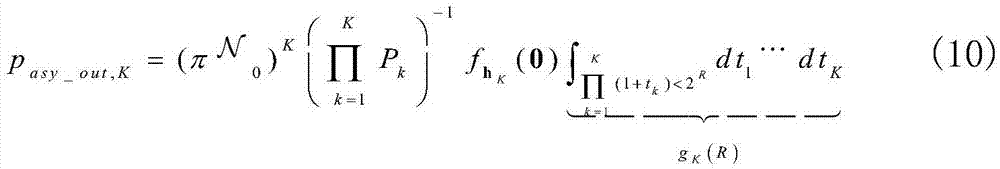
其中，g_K(R)可以表示为

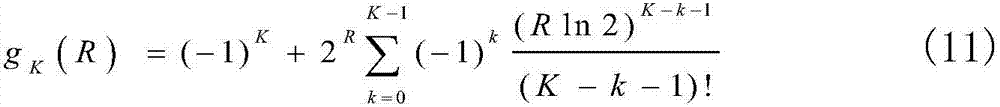
且g_K(R)是R的增函数和凸函数。将(11)代入(10)得到

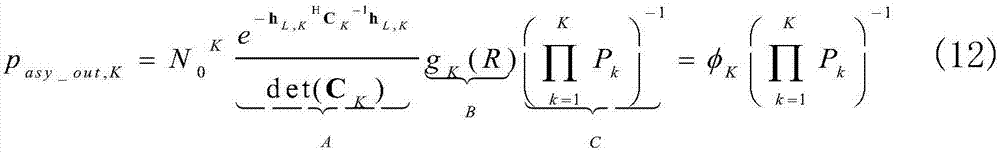
其中A，B和C分别代表时间相关性与直视直视、传输速率和发送功率对中断概率的影响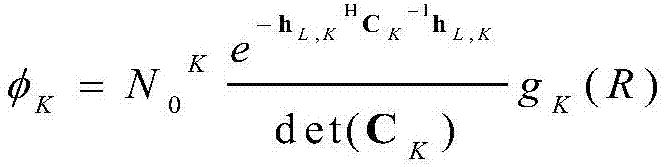，和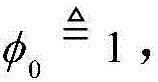渐近中断概率的简单形式不仅揭示了深刻的物理含义，而且有助于在相关莱斯衰落信道下的HARQ-IR系统的优化设计。通过图3验证了渐进中断概率分析的正确性。

2、基于吞吐量最大化的渐近中断概率

在评估单次HARQ传输吞吐量时，其性能指标通常采用有效吞吐量，它被定义为传输速率和成功概率的乘积，即T_g＝R(1-p_out,K)，理论证明在渐近意义上有效吞吐量等价于传统平均吞吐量的的吞吐量，即高SNR或低中断。因此，将有效吞吐量作为优化问题的目标函数也非常有意义。更具体地说，通过联合优化传输速率R和功率P₁,…,P_K来达到有效吞吐量的最大化。同时为了保证能量效率不至于过低，这里对传递每个消息的平均总发送功率加以约束，如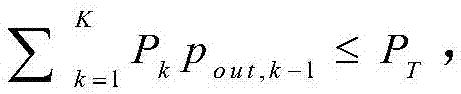其中P_T表示平均总发送功率的阈值，同时按照惯例定义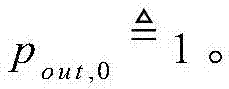因此，T_g的最大化问题可以构建成：

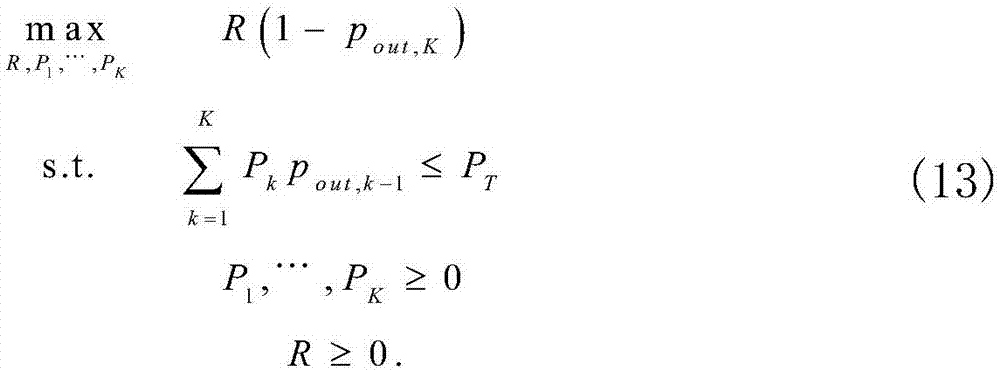
为了得到闭合解和简化计算复杂度，这里采用渐近中断概率来推导(13)的最优解。

2.A、问题分解

为了进行优化求解，p_{asy_out,K}的特殊且紧凑形式，激发将(13)分解成两个子问题，即最佳功率分配和最优速率选择，具体方法如下：

1)最佳功率分配：给定固定传输速率R，传输功率P₁,…,P_K可以先进行优化。由于(13)中目标函数仅仅中断概率含有发送功率，因此可以将(13)中的最佳功率分配重新写成：

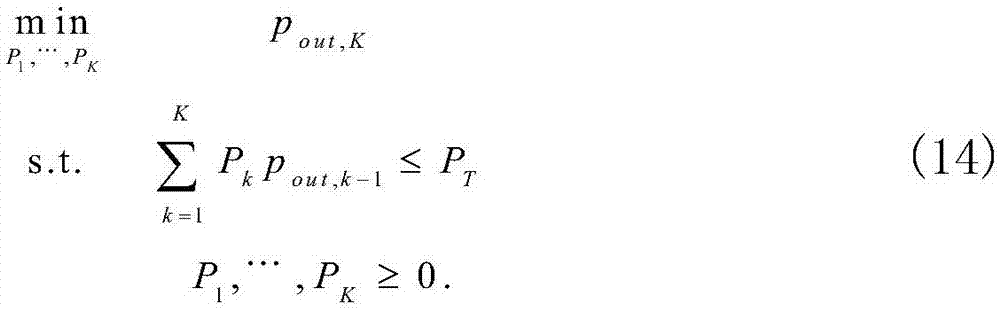
根据KKT条件，最优发射功率可以推导为：

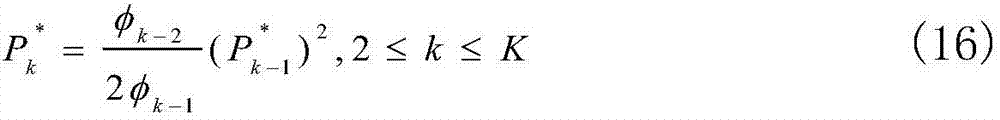
此时，最优发送功率均表示为R的函数，因此将最优发送功率代入到趋近性中断概率，p_out,K可以表示成：

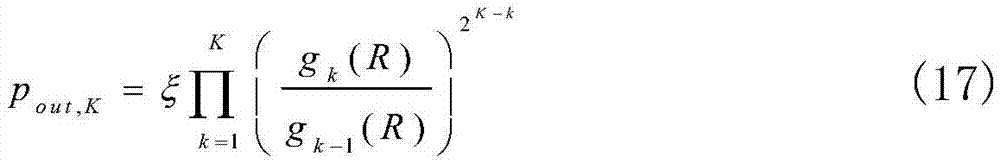
其中，ξ与R无关且

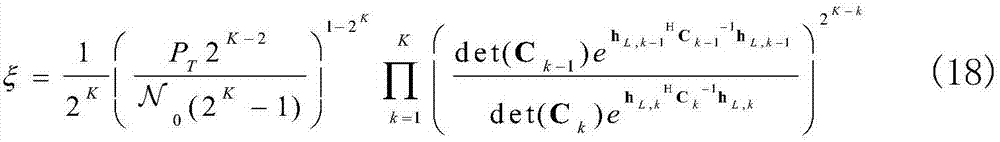
显然，(17)是P_T的递减函数，最终导致吞吐量增加。

2)最佳速率选择：在确定最佳发射功率后，第二个子问题致力于最优速率选择以最大化T_g。根据(13)和(17)，最佳传输速率可以选择为：

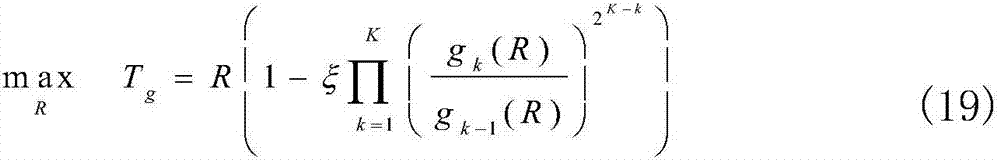
s.t.R≥0.

由于(19)是单变量优化问题，因此可以借助很多成熟优化工具进行数值求解。但由于目标函数的复杂形式，导致求解闭合形式的最优传输速率是不可能的，这阻碍了进一步揭示推导结果的物理内涵。因此，这里采用吞吐量上下限来来缩放优化问题，从而得到近似闭合解。为此，利用以下不等式：

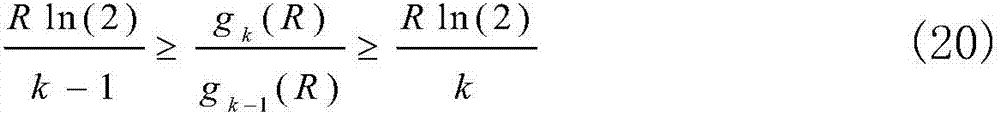
以(20)的左侧不等式为例，利用它可以得到吞吐量的下界，具体如下，当2≤k≤K时，应用不等式至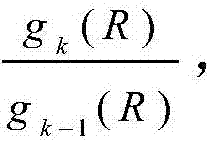则得到吞吐量的下界如下：

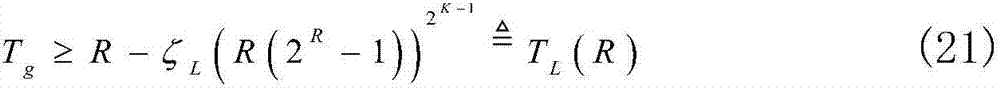
其中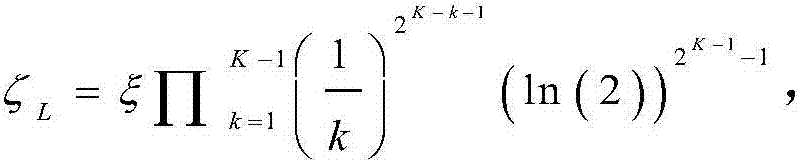T_L(R)表示最优吞吐量的下界。将(19)中的T_g替换为下界T_L(R)，最优化问题可以放缩为

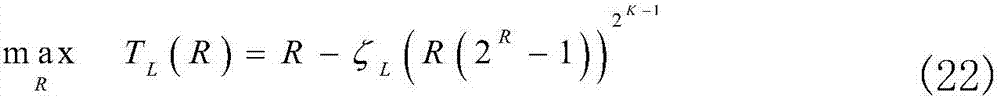
s.t.R≥0.

令T_L(R)对R的一阶导数为零，对应的解即是最优传输速率，即

其中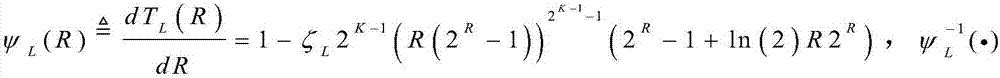表示ψ_L(R)的反函数。

此外，(23)意味着最优传输速率是ψ_L(R)的零点。值得一提的是，零点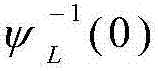是唯一存在的，因为ψ_L(R)是R的递减函数。

同样，应用(20)的右侧不等式可以得到最优吞吐量的上界，即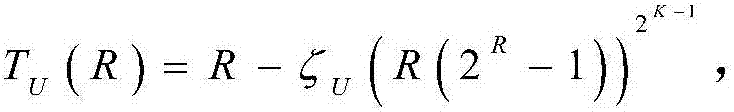其中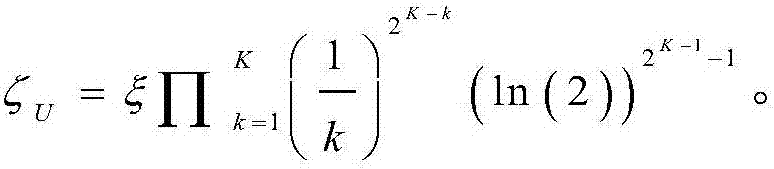，同样地，相应的最优传输速率可以表示成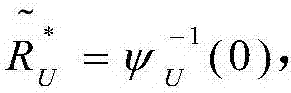其中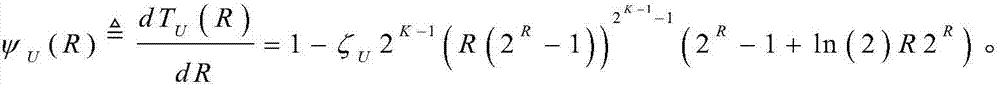

在确定完传输速率和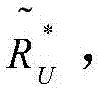最优吞吐量的相应下界和上界分别由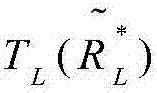和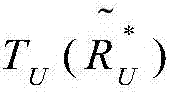给出。显然，(20)中的原始两个不等式意味着实际最优吞吐量满足如下不等式：

2.B、讨论

即使2.A节提供了一种分析方法来获得最佳发送功率和传输速率，但是近似的最优传输速率依然非常繁琐，因此不利于进一步获得一些简单形式结论。为进行后续渐近分析，可以应用如下引理中关于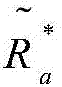的渐近性质。

引理1.在大总平均发射功率约束时P_T，即高SNR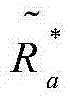，可以渐近地近似表示成如下下界：

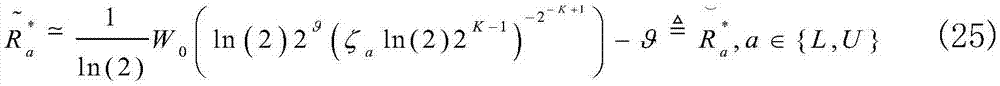
其中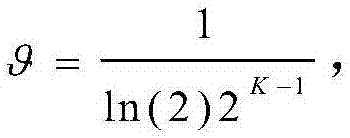，W₀(·)表示lambert-W函数的上分支。

利用该引理，可以得到高信噪比状态下最优吞吐量上下界的渐近表达式。

定理1.在高SNR条件下，即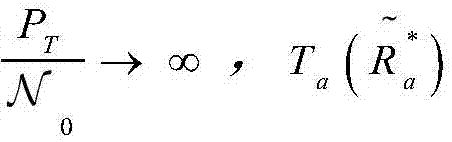趋近于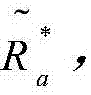意味着p_out,K→0，且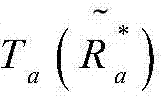渐近于：

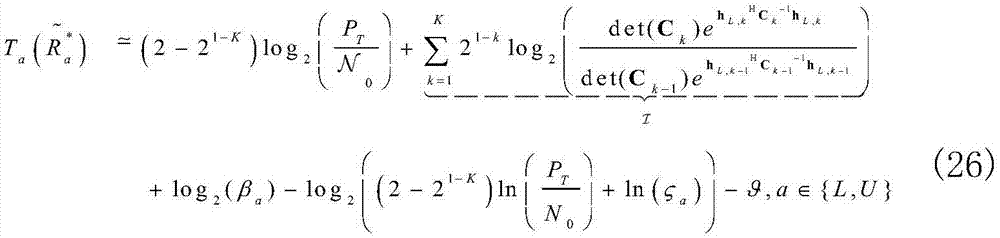
其中，

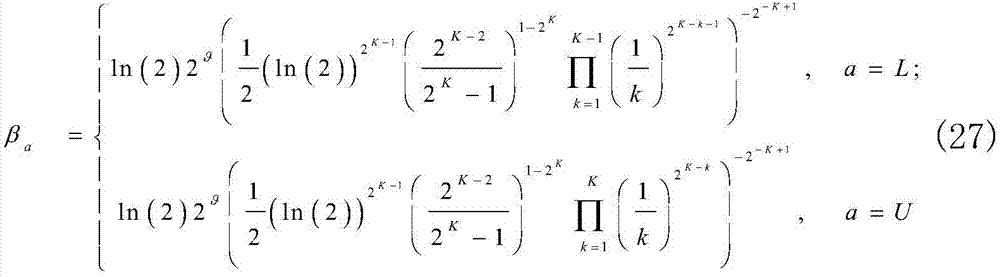
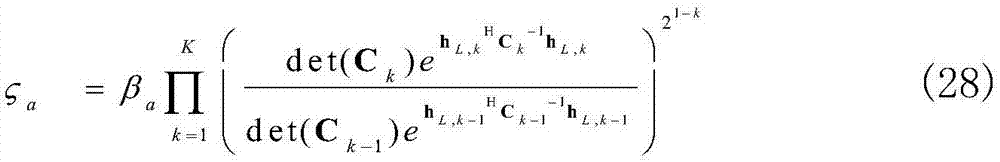
且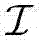主导了时间相关性和直视链路的影响。

这个定理不仅揭示了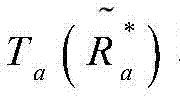相对于发送信噪比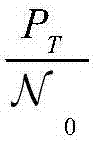的斜率，而且还量化了时间相关性和直视路径对吞吐量的影响，对应如下两个结论所总结。

利用两边夹定理至(24)，可以得出：

将(26)代入(29)，然后获得吞吐量相对于信噪比的斜率：

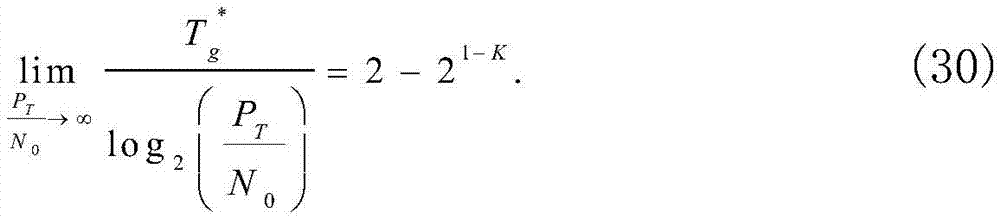
于是，如下结论1总结了最优吞吐量的标度定律。

结论1.在高SNR条件下，最优吞吐量遵循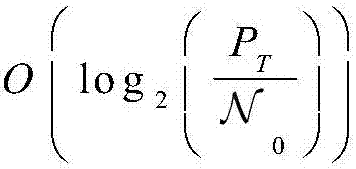的标度定律，斜率是2-2^1-K，O(·)表示同阶无穷大符号。显然，随着最大传输次数K增加到无穷大，吞吐量随着SNR的增长斜率从1增加到2。

此外，(26)右边的第二项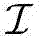主导了时间相关性和直视路径的影响。然而，相关矩阵C_K和直视信道系数h_L,K对最优吞吐量的影响密切相关，这也使得对它们的分析变得复杂。于是，这里分别讨论这两种影响因素对系统吞吐量的影响，即通过假设不存在直视链路来研究时间相关性的影响，和在忽略信道相关性的情况下讨论直视链路的影响。最终，可以得到如下结论

结论2.时间相关性对最佳吞吐量有不利影响，而最佳吞吐量可受益于直视链路。

最后为了凸显本发明所提出优化算法的有效性，这里采用与平均功率分配算法相对比，即假定每次发送功率都是恒定的。通过图4可以清楚看出所提出算法在高信噪比时吞吐量存在明显的间距，因此说明了所提出算法的优越性能，即所提出算法可以有效利用信道状态信息的统计特征来提高系统吞吐量。

综上所述，理论和数值分析结果显示在严格的中断约束或者高信噪比条件下，本实施例所提出解决方案与仿真结果一致，其中严格的中断概率约束符合在实际应用中要求，因此该方案是行之有效的一种改善功率效率的途径。本实施例的功率效率最大值的理论结果也为实际的系统设计提供了非常有意义的应用指导和参考价值。

上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。